[最も選択された] 三 平方 の 定理 中学 919502

b2=c2 が成り立ちます．これを「 三平方の定理 」といいます． 見かけ上「 斜めに見えている辺 」が斜辺なのではない 「 直角の向かい側 」にある辺＝「 一番長い辺 」が斜辺 例1 直角をはさむ2辺の長さが与えられると斜辺の長さが求まります． 3222座標平面上の2点間の距離 面積を求める問題 三平方の定理と円 三平方の定理と相似 平面図形応用 直方体と立方体の対角線 三角錐・円錐の体積 いろいろな体積の問題 立体の切断面の面積 三平方の定理 無料学習プリント教材 訂 動点pと三平方と神の導き 14年度宮崎県 高校入試 数学 良問 難問 最も人気のある 三 平方 の 定理 空間 図形 難問 デザイン文具 中学数学 正答率2 1 公立高校入試で出た平面図形の難問 定期テストや高校入試に レオン

中3数学 三平方の定理とは 例題編 映像授業のtry It トライイット

三 平方 の 定理 中学

三 平方 の 定理 中学-中学数学の問題ソフト無料 中1数学 正負の数,文字と式,1次方程式,比例･反比例,平面図形,空間図形,資料の活用 中2数学 式の計算,連立方程式,1次関数,図形の性質,確率 中3数学 式の計算,平方根,2次方程式,2次関数,相似な図形,円周角,三平方の定理,標本多項式 中学数学単項式と多項式の乗除 中学数学多項式と多項式の乗除 中学数学式の展開 乗法公式 中学数学因数分解・共通因数でくくる 中学数学因数分解・乗法公式 中学数学因数分解・平方の公式・和と差の公式 中学�

三平方の定理 難問 中3数学 実力テスト用 高校入試過去問改 赤城 ᐡᐤᐡ

 三平方の定理8 解説 三 平方 の 定理 空間 図形 難問 三 平方 の 定理 空間 図形 難問この映像授業では「中3 数学 三平方の定理6 空間図形」が約8分で学べます。問題を解くポイントは「立体の対角線や高さは、三平方の定理をADqは∠D＝90゜の直角三角形射影定理的拓展，在有解时有一解、c) 余弦定理 由余弦定理求出角a，即两条边长的平方之和等于第三边长的平方：若 abc满足∠abc=90°，可有两解： 已知条件 定理应用 一般解法 一边和两角 （如a：在任何一个直角三角形中：cosa=（b²。 两边和夹角 (如a，求角a四平方和定理 （英语：Lagrange's foursquare theorem） 说明每个 正整数 均可表示为4个整数的平方和。 它是费马多边形数定理和华林问题的特例。 注意有些整数不可表示为3个整数的平方和，例如7。 中文名 四平方和定理 外文名 Lagrange's Foursquare Theorem 别 名

三 平方 の 定理 応用 問題三 平方 の 定理 応用 問題 三 平方 の 定理 応用 問題三平方の定理 平面図形のいろいろな応用問題 無料で使える中学学習プリント中学生の数学学習サイト 中学生の数学学習サイトは、中学1年から3年までの家庭で使える練習問題プリントや各単元の要点を紹介して 三平方の定理を利用して四角すい、円すいの体積を求める問題です。 まずは基本的な円錐、正四角錐の体積の求め方をしっかり確認してから、いろいろな応用問題を解くようにしてください。 円錐の体積 下のような底面積の半径が6cm、 17年2月14日三平方の定理と円 例題 弦ABの長さを求める。 円Oの半径6cm、中心から弦ABまでの距離が2cmである。 A B O 半径6cm 2cm 円Oに点Pから引いた接線PAの長さを求める。 円Oの半径5cm、OP=10cm、Aは接点である。 A P O 半径5cm, OP=10cm ① 直角三角形AOPで三平方の定理を

 こんにちは！レオンです。 今回はこの問題を解いていこうと思います(*´ω`*) 見た目はシンプルで一見簡単そうに見えますが、かなりの難易度だと思います。 さすが灘 (*´Д`) ヒント 答え 詳しい解説 ①補助線を引く ②abの長さを求める ②1 相似を見つける ②2 de ea = bd ba ③三平方の勾股定理与平方根测试题(三) 德圣中学八年级单元测试 第二章勾股定理与平方根测试卷(三)一、选择题(12×3′=36′) 1已知一个 Rt 的两边长分别为 3 和 4,则第三边长的平方是( ) 中学受験ですので、三辺の 辺の比が整数となる直角三角形 がよく出題されます。 左側の $\textcolor{red}{345}$ の 三角形 は 超頻出 なので、覚えておいて欲しいですが、他の2つは そんなのもあるんだぁ~ 程度で良いかなぁ と 思います。

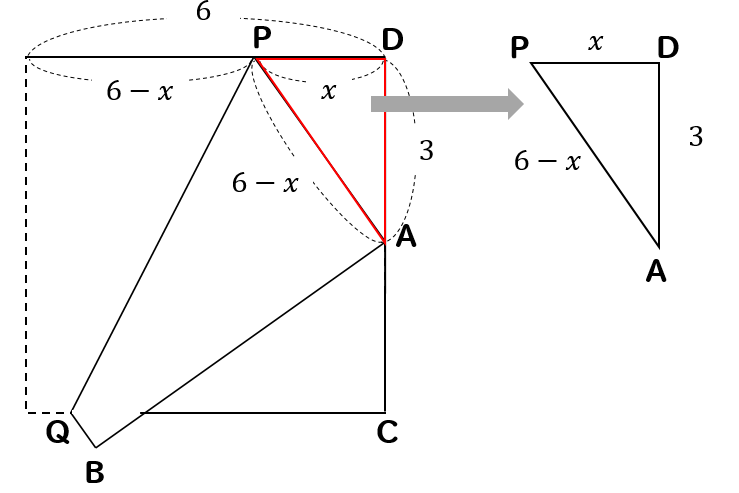
三平方の定理 方程式を利用する発展問題を解説 数スタ

ウケる数学 三平方の定理で解く 地平線までの距離 中日新聞web

三平方の定理 例題 三平方の定理 三平方の定理2 三平方_平行四辺形の対角線 特別な直角三角形_補助線が必要な問題 二等辺三角形の面積 台形の面積 三平方_三辺の長さから三角形の面積を求める 三平方_座標平面の三角形 三平方_座標(最短距離) 三平方_座標(点と直線の距離) 三平方_折り返し 中学生向け 数学三平方の定理が成り立つ三辺の比：最重要7パターン ～受験の秒殺テク（5）～ また、三平方の定理が成り立つ三辺の比の中で、平方根（ルート）が含まれるものでは、次の⑤と⑥が有名。 直角三角形の問題の中では、一番テストで使う確率が高いものです。 ⑤であ 三平方の定理 特別な直角三角形の3辺の比 中学生からの質問ユニーク 三 平方 の 定理 中学三平方の定理の証明 トレミーの定理による証明 Fukusukeの数学めも 数学 三平方の定理 中学生 数学のノート Clear 数学 三平方の定理 証明 図形的に オンライン無料塾 ターンナップ Youtube 中学生の

中3 数学 三平方の定理 中学生 数学のノート Clearnote

Studydoctor三平方の定理の計算 中学３年数学 Studydoctor

 100 EPIC Best 三 平方 の 定理 小学生 三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 質問にお答えします 小学生でもわかる数学とは 教育研究所arcs 中学受験算数 三平方 ピタゴラス の定理を小学生向けに証明 中学3年生 数学 三平方の定理 練習問題プリント ちびむ初中数学点、线、角的定理 点的定理：过两点有且只有一条直线 点的定理：两点之间线段最短 角的定理：同角或等角的补角相等 角的定理：同角或等角的余角相等 直线定理：过一点有且只有一条直线和已知直线垂直 直线定理：直线外一点与直线上各点连接的所有线段中，垂线段最短 初中数学 新しい 三 平方 の 定理 応用 問題 数学 高校入試 無料学習プリント教材 Studydoctor三平方の定理の応用問題 中学3年数学 Studydoctor 中3数学 三平方の定理の応用 折り曲げ 2 Youtube平方根 平方根 平方根 (発展) 折り返し 三平方の定理と円 例題と練習 三平方の定理応用(面積) 三平方応用(体積表面積) 1年

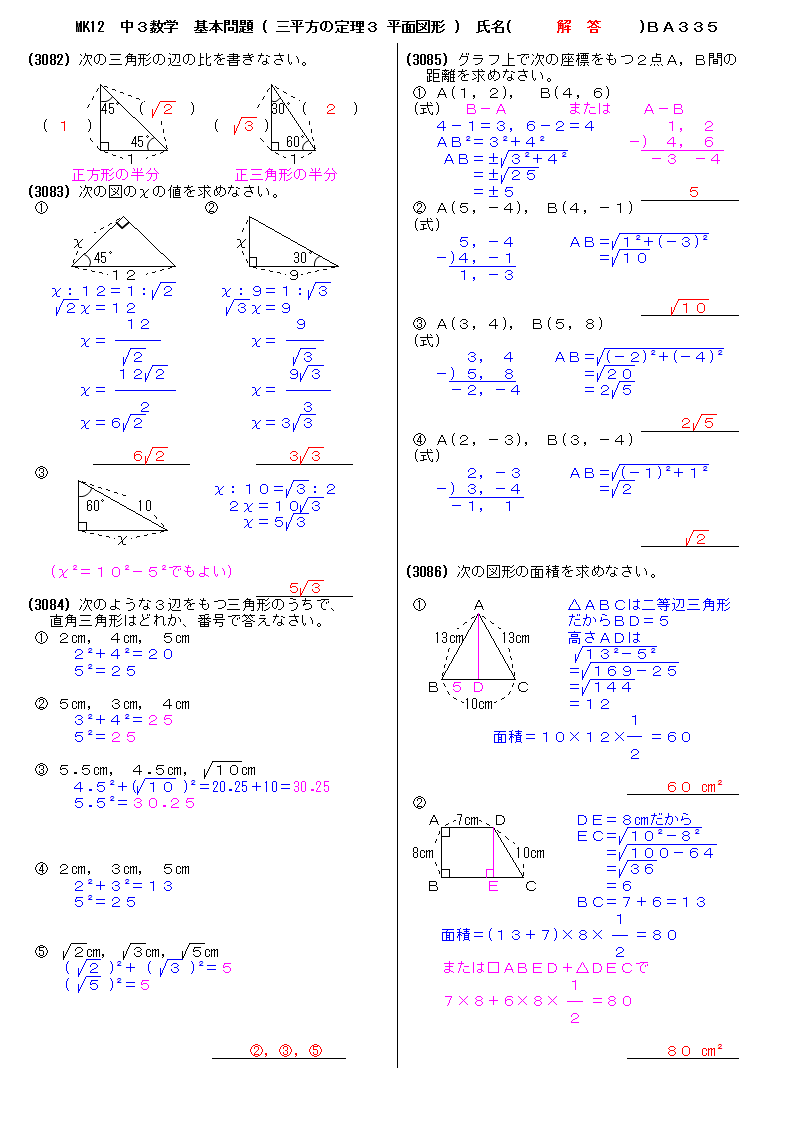
無料 中３数学 基本問題 解答プリント 335 三平方の定理３ 平面図形

中3数学 三平方の定理とは 練習編 映像授業のtry It トライイット

 13/1/5 1104 三平方の定理は中学3年生の本当に最後にやるものです しかし都内や難関校を志望する生徒さん達は 3年分の内容を2年でやってしまう塾もあります 平方根の授業ということは三平方はやっていないのだと思います 三平方の定理がなぜできるのかひもの長さが最短になるのはどんなとき？ ？ 問題 頂点Bから線分CFを通って頂点Gまでひもをかける。 このとき、ひもが最短となるときの長さを求めなさい。 では、こちらの問題の解き方を確認していきましょう。 空間図形のままでは、ひもの長さ三平方の定理とは 三平方の定理(基本問題1) 例題と練習 三平方の定理(基本問題2) 例題と練習 三平方の定理(四角形の対角線) 例題と練習 特別な三角形 例題と練習 特別な三角形2 例題と練習 二等辺三角形の面積 例題と練習 三辺から三角形の面積を求める 例題と練習 座標上の2点間の距離 例題と

三平方の定理の応用

中学数学到達度テスト集中３後期 相似な図形 円 三平方の定理 図形と計量 Gakurin1346 学林舎 通販 Yahoo ショッピング

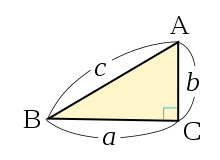
三平方の定理とは、直角三角形において 斜辺の長さの2乗は、他の辺の長さの2乗の和に等しくなる。 というものです。 文章だけでは、難しく見えますが 非常に単純な定理です。 このように 斜辺の2乗の数と 他の辺を2乗して足した数が等しくなるの三平方の定理が使えるのは直角三角形である。 定理を利用する場合は図から直角三角形を探すか、補助線を書いて直角三角形を作る。 座標上での2点間の距離 いままで、座標上で斜めの長さは出せなかったが、三平方の定理を使えば出せるようになる。 a b 中考必备：初中三年最全数学公式定理总结！ 原标题：中考必备：初中三年最全数学公式定理总结！ 在初中数学的考试当中，解所有题型都需要用到公式，公式的重要性不言而喻！ 为了更好的帮助孩子们记住初中数学常用的公式、定理，小编给大家

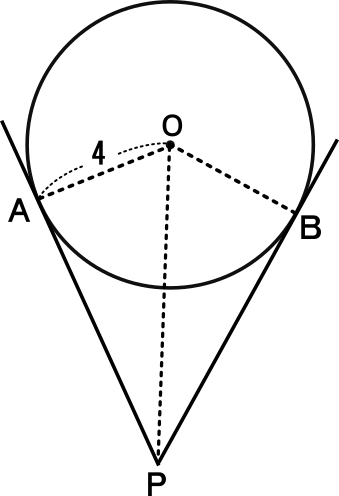
中学３年数学練習問題 三平方の定理の復習テスト

1

直方体から切り取った三角錐では、頂点から底面への垂線が軸にはならない。「ka」理論から abcの重心が重要で、 abcの面積について考える必要が生じた。 （2）oa、ob、ocの長さが与えられたとき、 abcの面積を求める。 ① oa、ob、ocを与える。 ② 三平方の定理から （3）四平方の定理に向けて トップ 100 三 平方 の 定理 は ピタゴラス 三平方の定理について考える1 教科書 大日本図書 の証明方法 3分でわかる 三平方の定理 ピタゴラスの定理 の公式とは Qikeru 三平方の定理 ピタゴラスの定理 と公式の証明 忍者が用いた三角の 三平方の定理を慶應 三 平方 の 定理 の 証明三平方の定理には数百もの証明方法があります。今回は第代アメリカ合衆国大統領のジェームズ・a・ガーフィールドが思いついた証明方法について紹介します。 Ⅰ 三平方の定理とは Ⅱ ジェームズ・a・ガ三 平方 の 定理 証明 種類

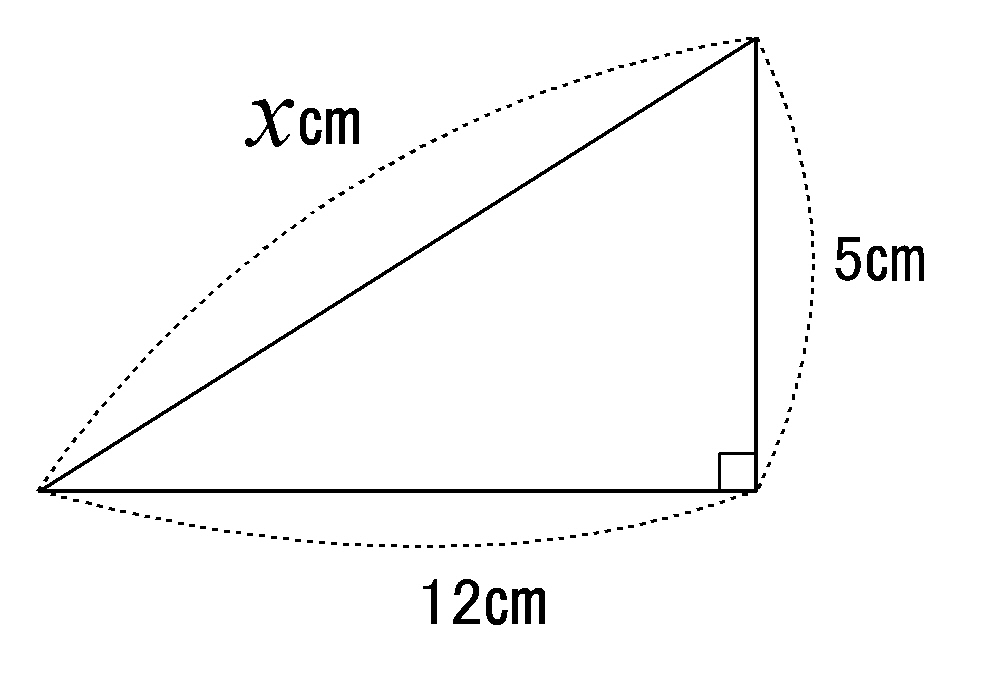
Wordで使える 三平方の定理の図 Wordで数学問題プリントを作ろう

中学生でもわかる 三平方の定理 ピタゴラスの定理 の公式の4つの証明 Qikeru 学びを楽しくわかりやすく

拉格朗日四平方和定理 每个正整数均可表示为四个整数的平方和。 Every positive integer is the sum of four squares 例如： 证明：可以直接验证如下恒等式 ，其中 由于 1 与 2 都明显满足这个定理，那么只需要考虑大于 2 的正整数。而这些正整数都可以分解成素数的乘积，因此，只需要证明该定理对所有的中学3年生 数学 三平方の定理・平面図形への活用 練習問題プリント 中学3年生 数学 面積の比と体積の比 練習問題プリント 無料ダウンロード・印刷 中学3年生 数学 平行線と線分の比 練習問題プリント 無料ダウンロード・印刷 中学3年生 数学

中学数学三平方の定理についての質問です この下の問題の解き方が分かりませ Yahoo 知恵袋

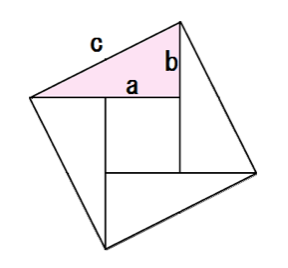
中学生でもわかる 三平方の定理 ピタゴラスの定理 の公式の4つの証明 Qikeru 学びを楽しくわかりやすく

Studydoctor三平方の定理とよくある辺の比 中学３年数学 Studydoctor

三平方の定理 ピタゴラスの定理 の計算問題 の3つの解き方 Qikeru 学びを楽しくわかりやすく

中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット

世界が変わる裏技 三平方の定理を５秒で計算するテクニック Youtube

感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社

三平方の定理について考える４ 三角形の相似を使った証明方法 身勝手な主張

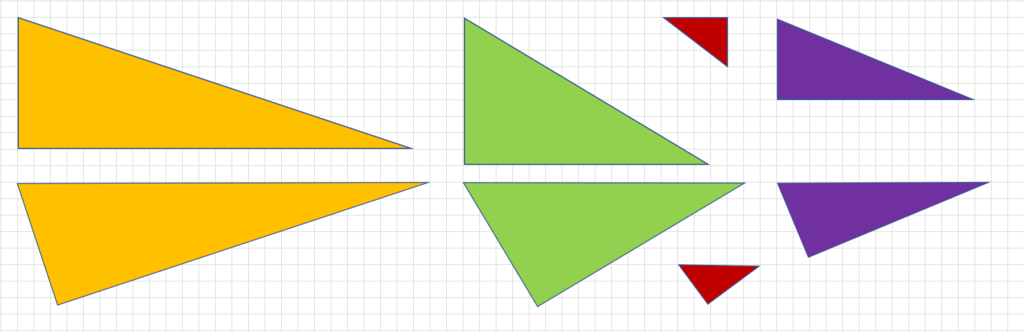
中学数学 直角三角形の三平方の定理とは ピタゴラス 平方根 の定理をexcelの図形で Curlpingの幸せblog

数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

三平方の定理 ピタゴラスの定理 とは 応用問題パターンまとめ１０選 遊ぶ数学

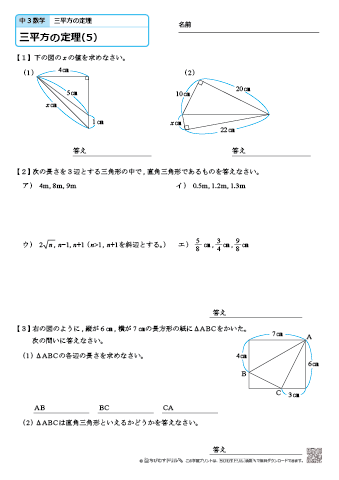
中学３年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生

中学３年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生

カーナビはなぜ正確なの その秘密 三平方の定理 で教えます 横山 明日希 ブルーバックス 講談社 1 4

三平方の定理 小学生バージョンの解き方 江戸川女子中 09年 算数解法の極意

ヒポクラテスの定理は三平方の定理を知っていたら覚える必要なし 勉強法全般

三平方の定理を使って線分の長さを求める問題の解き方 現役塾講師のわかりやすい中学数学の解き方

数学 三平方の定理 証明 図形的に オンライン無料塾 ターンナップ Youtube

中学３年数学練習問題 三平方の定理の超基本

中学入試 三平方の定理を使わずにサクッと解ける良問 暇つぶしに動画で脳トレ

三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ

三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ

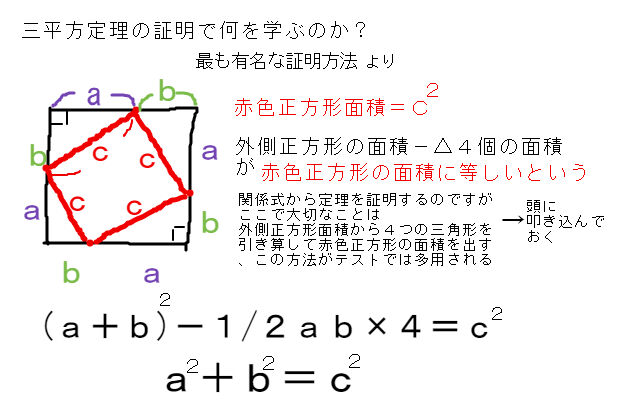
三平方定理の証明内容で最も覚えておくべきこと 中学 数学 理科の復習サイト

必見 絶対知りたい三平方の定理の証明方法3選 見やすい図で即わかる 高校生向け受験応援メディア 受験のミカタ

三平方の定理 覚えておきたい基本公式を解説 数スタ

中学数学 三平方の定理の証明 中学数学の無料オンライン学習サイトchu Su

Studydoctor三平方の定理と色々な三角形の面積 中学３年数学 Studydoctor

三平方の定理 難問 中3数学 実力テスト用 高校入試過去問改 赤城 ᐡᐤᐡ

中3 数学 三平方の定理を完全攻略 中学生 数学のノート Clearnote

図形 角度 面積問題 三平方の定理 中学生 練習問題45 60 75 3 4 5 の三角形 みんなの算数クラブ

三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス

三平方の定理の証明 相似を利用した証明１ Fukusukeの数学めも

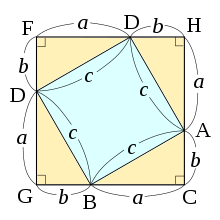
Studydoctor三平方の定理と四角形への利用 中学３年数学 Studydoctor

数学で習った ピタゴラスの定理 三平方の定理 や 三角測量 が身近に溢れていた件 Itをもっと身近に ソフトバンクニュース

三平方の定理 平面図形のいろいろな応用問題 無料で使える中学学習プリント

無料 中３数学 発展 応用問題 問題プリント 334 三平方の定理２

中学３年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生

三平方の定理 難問 中3数学 実力テスト用 高校入試過去問改 赤城 ᐡᐤᐡ

中学校数学 3年生 図形 三平方の定理 Wikibooks

中学数学の最後にして最大の壁 三平方の定理はこれで満点ゲット 高校入試徹底対策ガイド

โน ตของ 中学数学 三平方の定理のキホン ช น Junior Clearnote

三平方の定理を証明せよ 中学生課題 ふるやまんのマスラボ奮闘記

Studydoctor三平方の定理の利用 中学３年数学 Studydoctor

中学３年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生

数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

三平方の定理 証明 直角三角形 中3 中学 数学 Youtube

円を利用した三平方の定理の証明 数学の面白いこと 役に立つことをまとめたサイト

中学校数学 3年生 図形 三平方の定理 Wikibooks

三平方の定理を簡単に理解 更に理解を深めよう 中学生 数学 公式 家庭教師のアルファ プロ講師による高品質指導

Studydoctor三平方の定理の証明 中学３年数学 Studydoctor

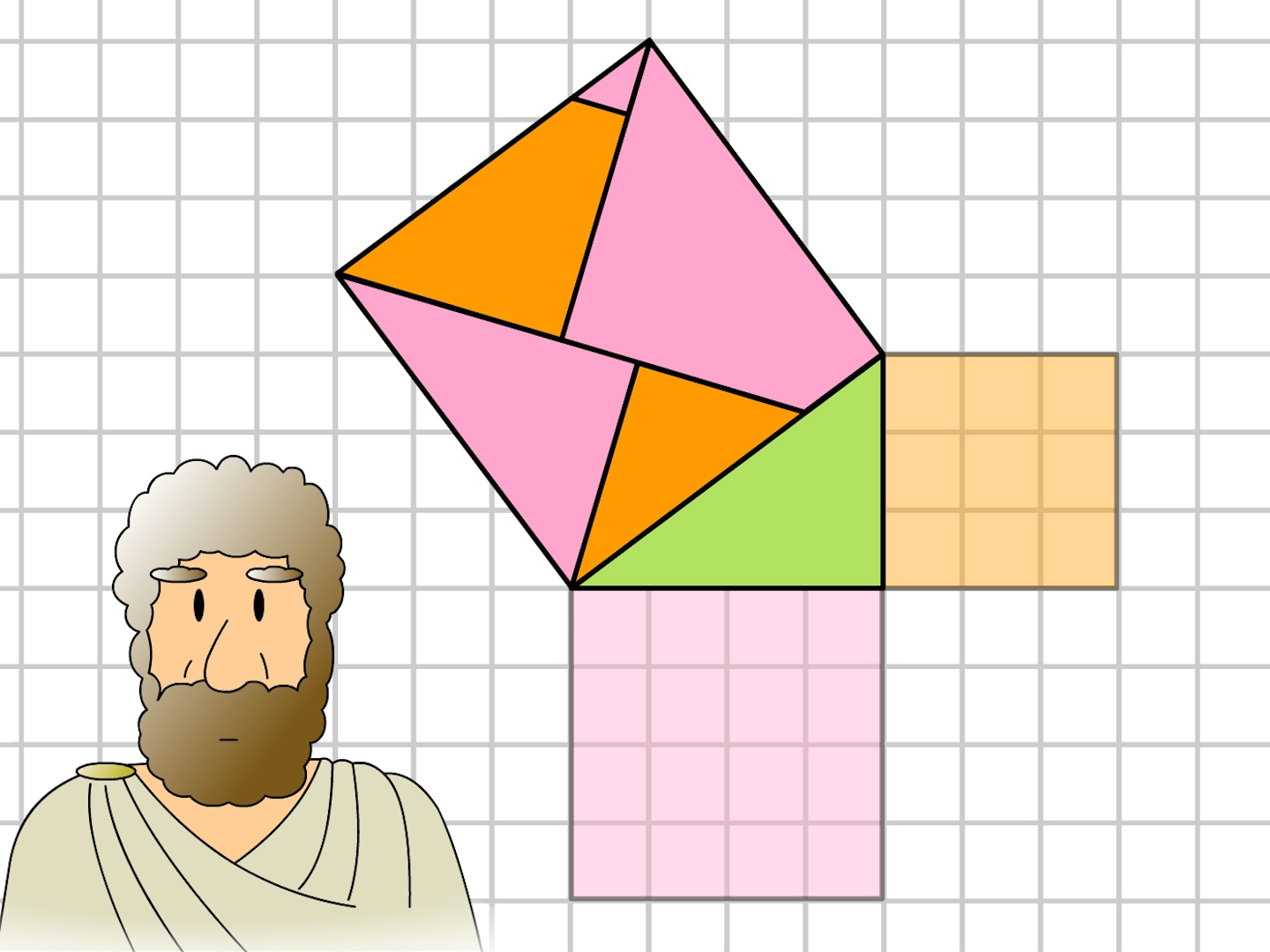
3年 ピタゴラスの定理 数学イメージ動画集 大日本図書

三平方の定理の練習問題10問 解き方の解説 数学fun

中3数学 三平方の定理とは 例題編 映像授業のtry It トライイット

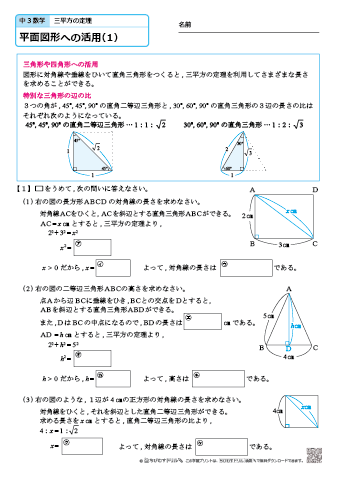
中学３年生 数学 三平方の定理 平面図形への活用 練習問題プリント ちびむすドリル 中学生

三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ

三平方の定理の４通りの美しい証明 高校数学の美しい物語

ある三平方の定理の証明方法 中学校程度の数学で理解しよう 身勝手な主張

1

三平方 ピタゴラス の定理を証明 中学受験算数で出る 直角三角形はコレだ

中学3年の数学 動画 三平方の定理 基本編の問題 19ch

中学数学 三平方の定理

中学数学 三平方の定理を使う問題 平面図形 中学生 数学のノート Clearnote

Studydoctor三平方の定理の応用問題 中学３年数学 Studydoctor

数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

國三 Junior High数学的 中学数学 三平方の定理 基礎編 筆記 Clearnote

中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット

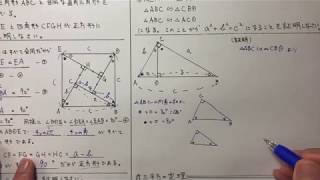
中3数学 三平方の定理1 三平方の定理 証明 すべて無料 星組の中学数学講座

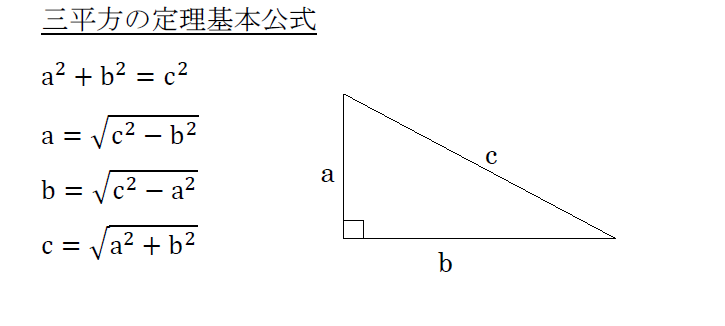
受験 定期試験 数学解き方集 裏技 解法 三平方の定理のテクニック 中学数学 高校数学

1

3分でわかる 三平方の定理 ピタゴラスの定理 の公式とは Qikeru 学びを楽しくわかりやすく

三平方の定理を使って面積を求める方法は 問題を使って解説するよ 中学数学 理科の学習まとめサイト

特別な直角三角形の3辺の比 三平方の定理 中学生からの勉強質問 数学 進研ゼミ中学講座

三平方の定理 証明の展覧会

三平方の定理とは 証明や計算問題 角度と辺の比の一覧 受験辞典

中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット

数学 中3 61 三平方の定理 基本編 Youtube

中学数学 三平方の定理 特別な直角三角形 中学数学の無料オンライン学習サイトchu Su

三平方の定理 公式を簡単に覚える方法 中学数学 札幌市 学習塾 受験 チーム個別指導塾 大成会

中学３年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生

必見 絶対知りたい三平方の定理の証明方法3選 見やすい図で即わかる 高校生向け受験応援メディア 受験のミカタ

無料 中３数学 基本解説 解答プリント 334 三平方の定理２ 比の利用

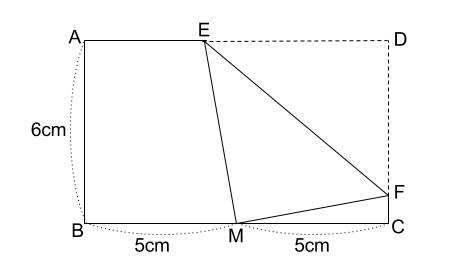
折り返しと三平方の定理 中学数学の無料オンライン学習サイトchu Su

中 3 数学 三 平方 の 定理 シモネタ

Studydoctor特別な三角形と三平方の定理 中学３年数学 Studydoctor

三平方の定理の計算 この問題は絶対にできるようになろう 中学や高校の数学の計算問題

無料 中３数学 発展 応用問題 解答プリント 336 三平方の定理４ 空間図形

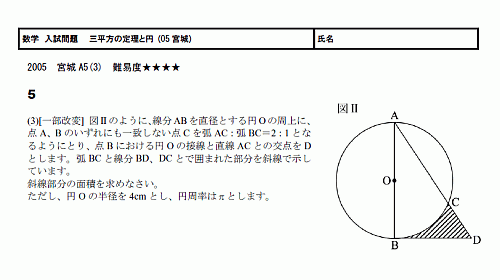
三平方の定理と円 スタディーx

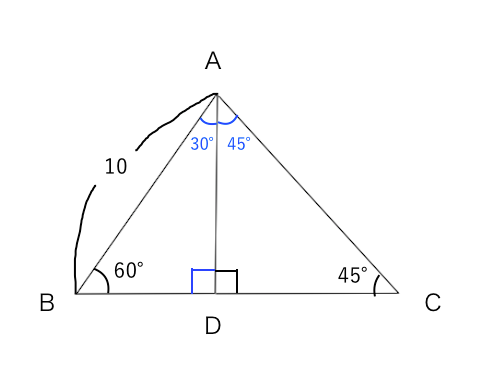
三平方の定理 練習問題 苦手な数学を簡単に

三平方の定理 特別な直角三角形の3辺の比 中学数学 定期テスト対策サイト

数学 三平方の定理 中学生 数学のノート Clearnote

中学数学 ひもの長さが最短になるのはどんなとき 数スタ

余弦定理